Title page

会议:Accepted at CVPR 2022
年份:2022
github链接:https://github.com/xiaoachen98/DALN
pdf链接:http://arxiv.org/abs/2204.03838
Summary
-
现有的对抗UDA(unsupervised domain adaptation)方法通常采用额外的判别器来与特征提取器进行极小-极大博弈。然而,大多数这些方法未能有效利用预测的鉴别信息,从而导致生成器的模式崩溃。
UDA: transfer knowledge from a labeled source domain to an unlabeled target domain in the presence of a domain shift
-
该文章设计了一种简单而有效的对抗范式,即去除鉴别器的对抗学习网络(DALN),其中类别分类器被重复使用作为鉴别器,通过统一的目标实现明确的域对齐和类别区分,使DALN能够利用预测的鉴别信息实现足够的特征对齐。
-
引入了Nuclear-norm Wasserstein discrepancy (NWD),这种NWD可以与分类器相结合,作为一个满足K-Lipschitz约束(https://zhuanlan.zhihu.com/p/520107941)的鉴别器,无需额外的weight clipping或gradient penalty策略。

-
DALN在各种公共数据集上实现SOTA,而且作为即插即用(plug-and-play)的技术,NWD可以直接用作现有UDA算法的通用正则化器。
Introduction
-
UDA方法常采用学习domain-invariant特征表示的方法,具体可分为:
-
moment matching methods:通过匹配源域特征和目标域特征的定义明确的分布差异来显式减少域偏移
- DDC(Eric Tzeng, Judy Hoffman, Ning Zhang, Kate Saenko, and Trevor Darrell. Deep domain confusion: Maximizing for domain invariance. arXiv:1412.3474, 2014. 1, 2)通过最小化最大平均差异(MMD),显式地调整跨域的学习特征分布
- MK-MMD
- JMMD
- MDD
-
adversarial learning methods:implicitly mitigate the domain shift by playing an adversarial min-max two-player game
- An additional discriminator
- DANN: introduced an additional discriminator to distinguish the features generated by the feature extractor
- FGDA leveraged a discriminator to distinguish the gradient distribution of features
- DADA: couple the task-specific classifier with the domain discriminator to align the joint distributions of two domains
- Use two task-specific classifiers (called bi-classifier): MCD, SWD, CGDM
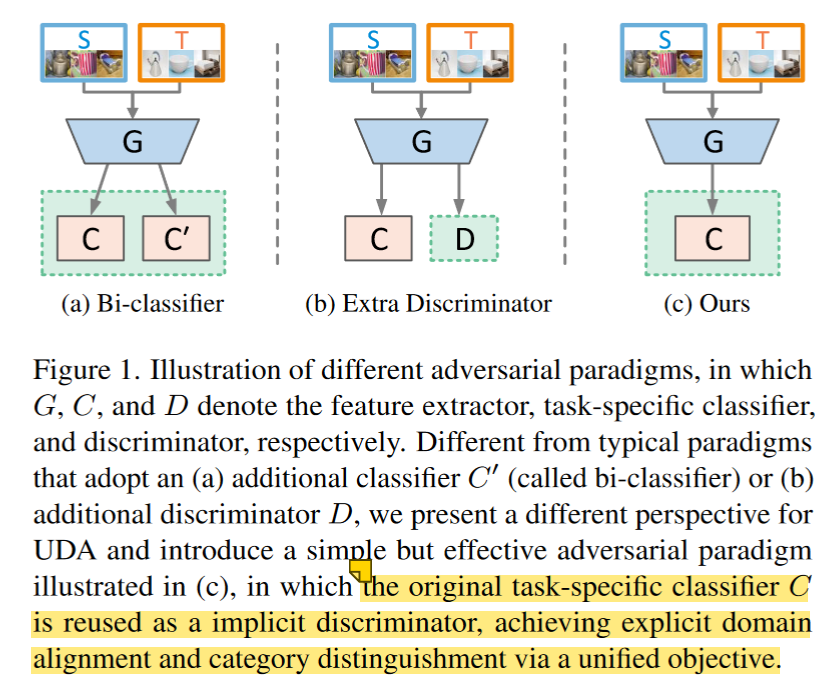
作者认为第一种和第二种模式通常关注domain级特征混淆,这可能会损害category级信息,从而导致模式崩溃问题。而模式三是在原始任务分类器加上一个discrepancy(NWD)作为discriminator/critic,通过统一的目标同时实现域对齐和类别区分,使模型能够利用预测的判别信息来捕获特征分布的多模态结构
- An additional discriminator
-
Workflow
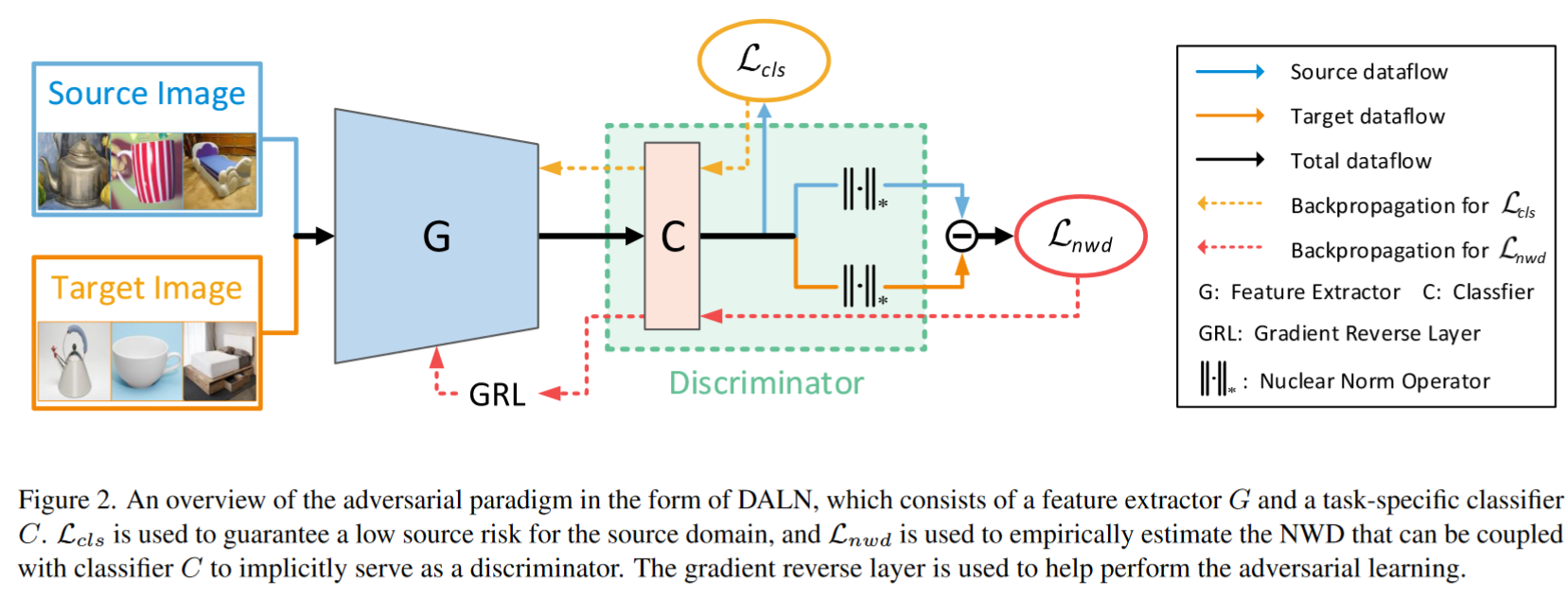
Methods
Recap of Preliminary KInowledge
发现:分类器C具有源域和目标域的隐式区分能力,可以直接用作鉴别器。

Reusing the Classifier as a Discriminator
Motivation Re-clarification
分类器具有隐式判别能力:对于源域,受益于监督训练,自相关矩阵的值集中在主对角线上。相反,对于目标域,由于缺乏监督,预测会在非对角线元素上产生更大的值。因此,自相关矩阵中表示的类内和类间相关性能够构建adversarial critic。
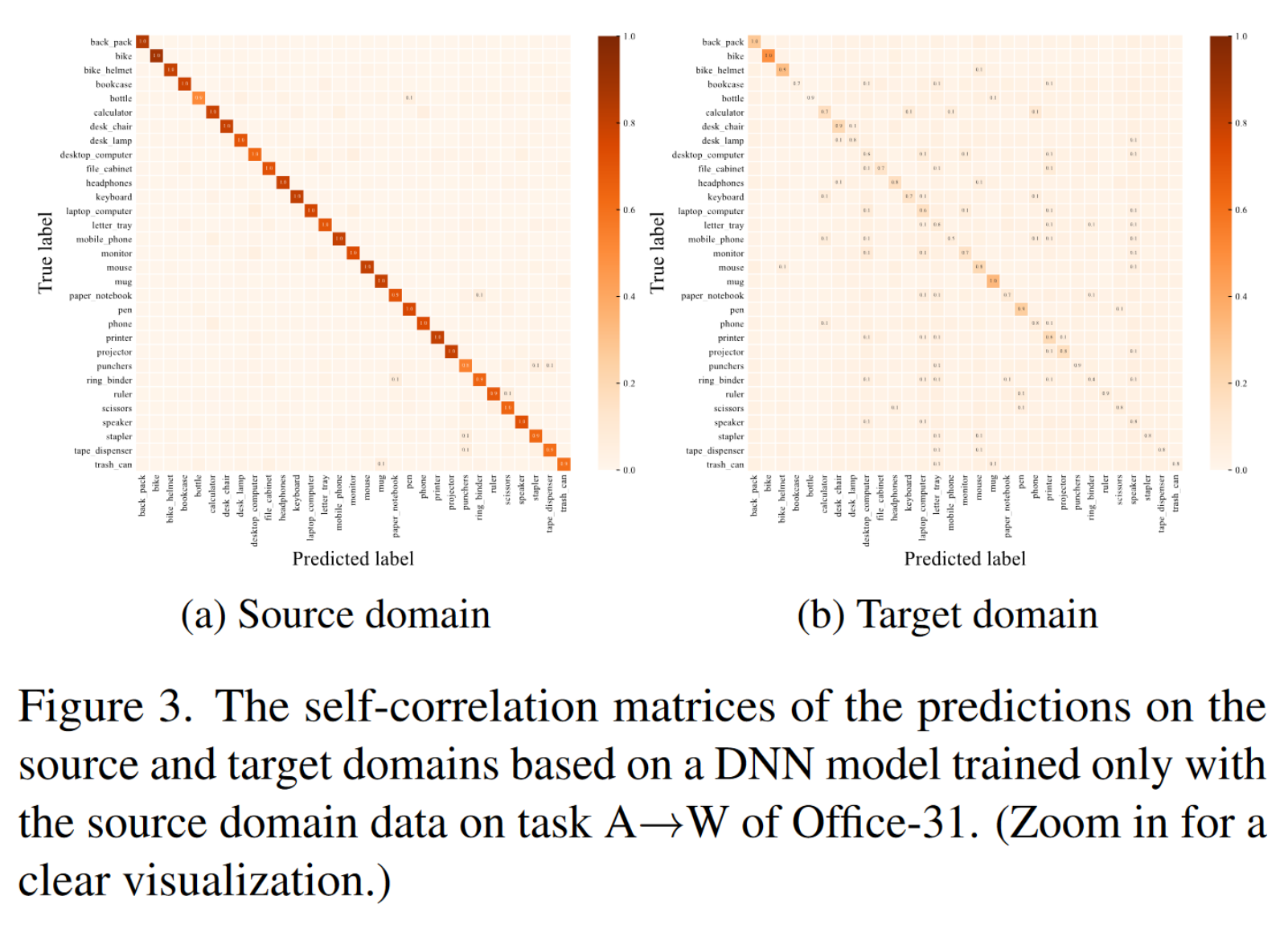
Rethinking the Intra-class and Inter-class Correlations.


From Correlations Critic to 1-Wasserstein Distance
核心:把WGAN中额外的Discriminator \(h\)直接改为分类器的Frobenius norm函数

Adversarial Learning with the NWD
From Frobenius Norm to Nuclear Norm
尽管\(D = ‖C‖_F\)可以进行生成对抗训练,但基于Frobenius-norm 1-Wasserstein distance的训练可能会倾向于将少样本类归类到临近的大样本类,从而降低预测多样性,因此作者引入了Nuclear norm来增加预测的多样性。
分类器由一个全连接层和一个 softmax 激活函数组成。可以证明我们的隐式鉴别器的所有组件都满足 KLipschitz 约束

由此,作者给出了domain critic损失函数:
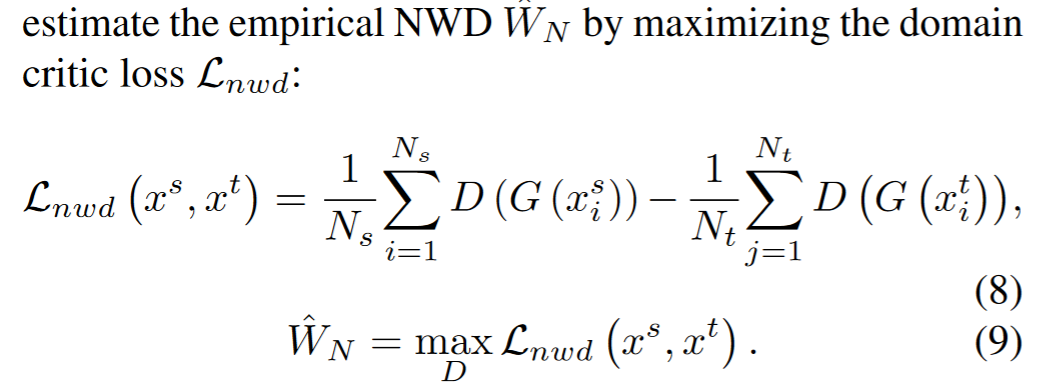
Adversarial Learning for DALN
-
本文中,作者构建了一个DALN模型
- 基于预训练 ResNet 的生成器 G
- 全连接层和 softmax 层构建的分类器 C 组成
- 为了避免 DALN 的繁琐交替更新,使用了gradient reverse layer (GRL) 梯度反向层 (GRL)
-
为了增加UDA分类的可信度,增加了对源域数据的分类损失函数
-
由此,损失函数如下:
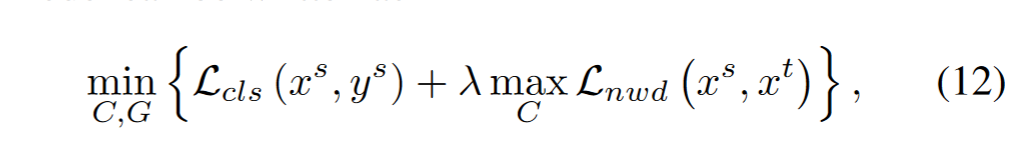
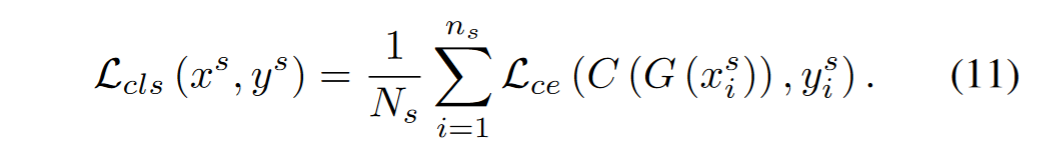
Result-show
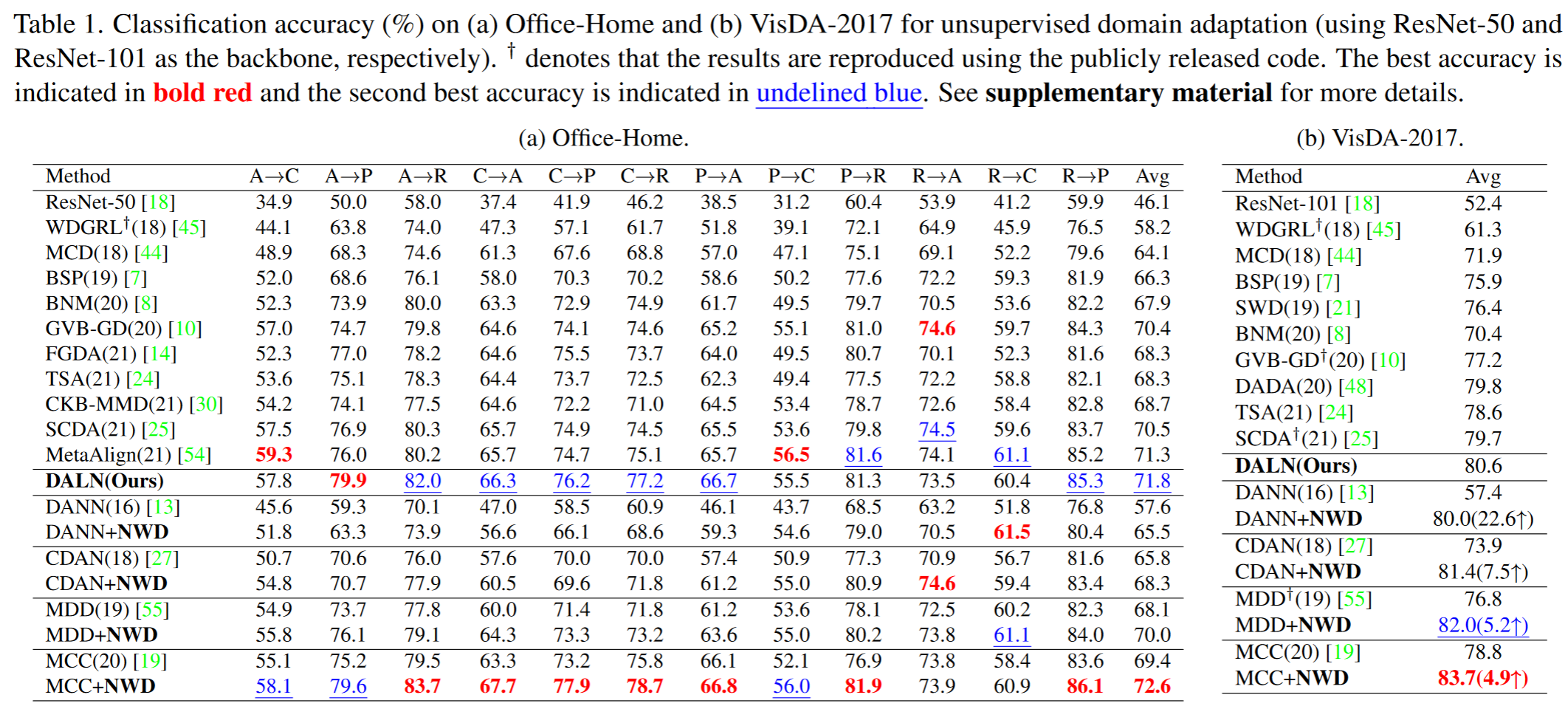
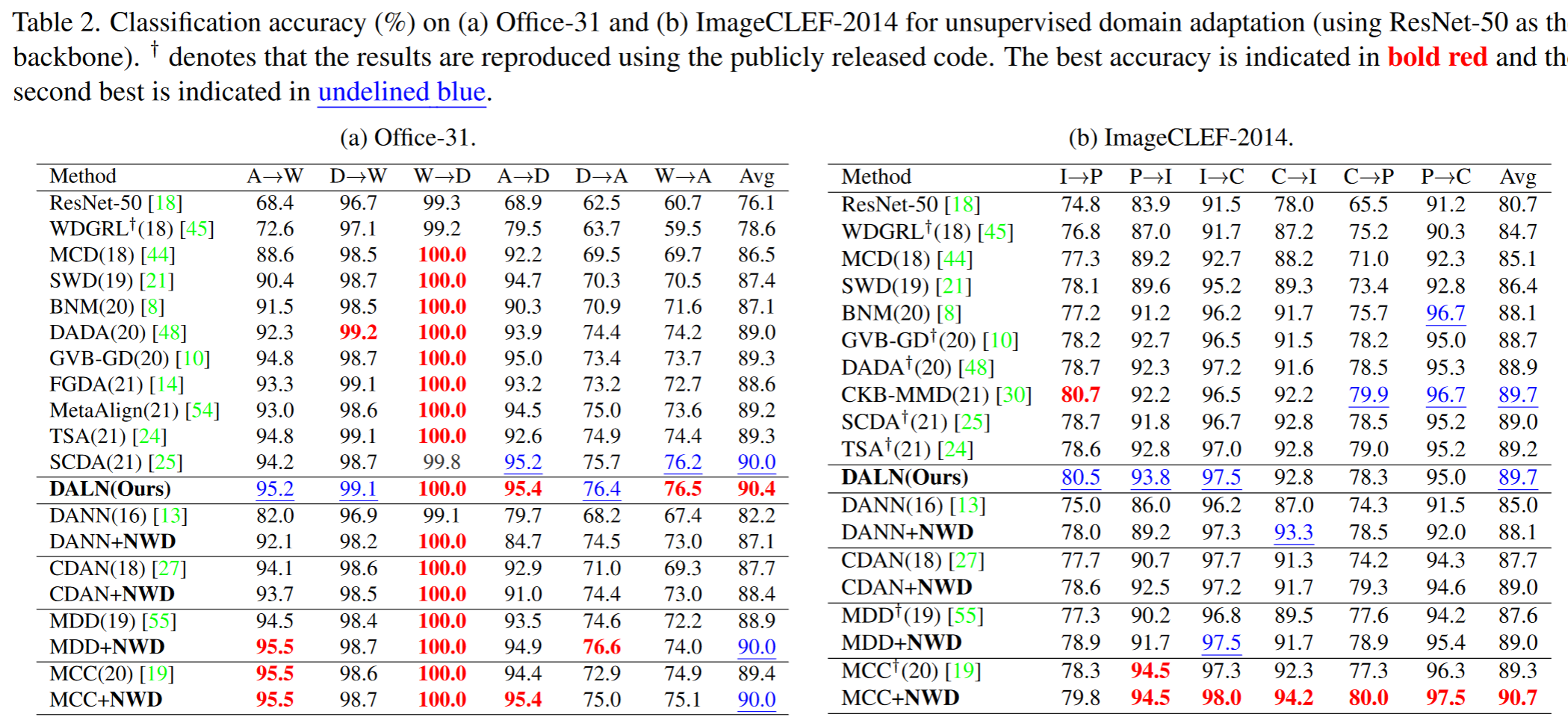
启发和思考
代码注释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
### Core code
from nwd import NuclearWassersteinDiscrepancy
# instantiate NWD
discrepancy = NuclearWassersteinDiscrepancy(classifier.head) # classifier is your own whole classification model
# compute output
x = torch.cat((x_s, x_t), dim=0)
y, f = classifier(x)
y_s, y_t = y.chunk(2, dim=0)
# compute cross entropy loss on source domain
cls_loss = nn.CrossEntropyLoss(y_s, labels_s)
# compute nuclear-norm wasserstein discrepancy between domains
# for adversarial classifier, minimize negative nwd is equal to maximize nwd
discrepancy_loss = -discrepancy(f)
transfer_loss = discrepancy_loss * trade_off_lambda # multiply the lambda to trade off the loss term
loss = cls_loss + transfer_loss
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
### nwd.py
import torch
import torch.nn as nn
import torch.nn.functional as F
from grl import WarmStartGradientReverseLayer
class NuclearWassersteinDiscrepancy(nn.Module):
def __init__(self, classifier: nn.Module):
super(NuclearWassersteinDiscrepancy, self).__init__()
self.grl = WarmStartGradientReverseLayer(alpha=1., lo=0., hi=1., max_iters=1000, auto_step=True)
self.classifier = classifier
@staticmethod
def n_discrepancy(y_s: torch.Tensor, y_t: torch.Tensor) -> torch.Tensor:
pre_s, pre_t = F.softmax(y_s, dim=1), F.softmax(y_t, dim=1)
loss = (-torch.norm(pre_t, 'nuc') + torch.norm(pre_s, 'nuc')) / y_t.shape[0]
return loss
def forward(self, f: torch.Tensor) -> torch.Tensor:
f_grl = self.grl(f)
y = self.classifier(f_grl)
y_s, y_t = y.chunk(2, dim=0)
loss = self.n_discrepancy(y_s, y_t)
return
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
### grl.py
from typing import Optional, Any, Tuple
import numpy as np
import torch.nn as nn
from torch.autograd import Function
import torch
class GradientReverseFunction(Function):
@staticmethod
def forward(ctx: Any, input: torch.Tensor, coeff: Optional[float] = 1.) -> torch.Tensor:
ctx.coeff = coeff
output = input * 1.0
return output
@staticmethod
def backward(ctx: Any, grad_output: torch.Tensor) -> Tuple[torch.Tensor, Any]:
return grad_output.neg() * ctx.coeff, None
class GradientReverseLayer(nn.Module):
def __init__(self):
super(GradientReverseLayer, self).__init__()
def forward(self, *input):
return GradientReverseFunction.apply(*input)
class WarmStartGradientReverseLayer(nn.Module):
"""Gradient Reverse Layer :math:`\mathcal{R}(x)` with warm start
The forward and backward behaviours are:
.. math::
\mathcal{R}(x) = x,
\dfrac{ d\mathcal{R}} {dx} = - \lambda I.
:math:`\lambda` is initiated at :math:`lo` and is gradually changed to :math:`hi` using the following schedule:
.. math::
\lambda = \dfrac{2(hi-lo)}{1+\exp(- α \dfrac{i}{N})} - (hi-lo) + lo
where :math:`i` is the iteration step.
Args:
alpha (float, optional): :math:`α`. Default: 1.0
lo (float, optional): Initial value of :math:`\lambda`. Default: 0.0
hi (float, optional): Final value of :math:`\lambda`. Default: 1.0
max_iters (int, optional): :math:`N`. Default: 1000
auto_step (bool, optional): If True, increase :math:`i` each time `forward` is called.
Otherwise use function `step` to increase :math:`i`. Default: False
"""
def __init__(self, alpha: Optional[float] = 1.0, lo: Optional[float] = 0.0, hi: Optional[float] = 1.,
max_iters: Optional[int] = 1000., auto_step: Optional[bool] = False):
super(WarmStartGradientReverseLayer, self).__init__()
self.alpha = alpha
self.lo = lo
self.hi = hi
self.iter_num = 0
self.max_iters = max_iters
self.auto_step = auto_step
def forward(self, input: torch.Tensor) -> torch.Tensor:
""""""
coeff = np.float(
2.0 * (self.hi - self.lo) / (1.0 + np.exp(-self.alpha * self.iter_num / self.max_iters))
- (self.hi - self.lo) + self.lo
)
if self.auto_step:
self.step()
return GradientReverseFunction.apply(input, coeff)
def step(self):
"""Increase iteration number :math:`i` by 1"""
self.iter_num += 1
